前言

上篇文章提過，線性模型的線性是指在參數上的線性（linear in parasmeters）。在此，對廣義線性回歸模型也是一樣。以下從兩個解釋變數的一階模型模型切入，揭開反應函數在三維空間下的面貌。並再增加解釋變數數量，介紹廣義線性回歸模型，把模型以矩陣型式表達後，利用最小平方法求取參數估計量，得到廣義線性回歸模型之最小平方估計量。

兩個解釋變數的一階模型

先使用一個比較簡單的模型來解釋線性回歸模型到底在求什麼，以及模型參數的涵義。假設有 2 個解釋變數 X1 與 X2，此時回歸模型

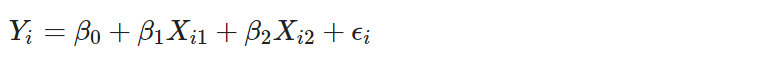
稱作具兩個解釋變數一階模型（a first-order model with two predictor variables）。其中一階模型係指解釋變數為線性，Xi 沒有次方或交互作用，而 $Y_i$ 為第 $i$ 次試驗的反應變數、Xi1$ 與 Xi2 為第 i 次試驗的兩個解釋變數、Betai, i=0, 1, 2 為參數、$\epsilon_i$ 為殘差項。

假設殘差項期望值為零，則反應函數之期望值

為一個三維度空間中的平面。把參數代入一組數值

為平面的法向量，反應函數如下圖

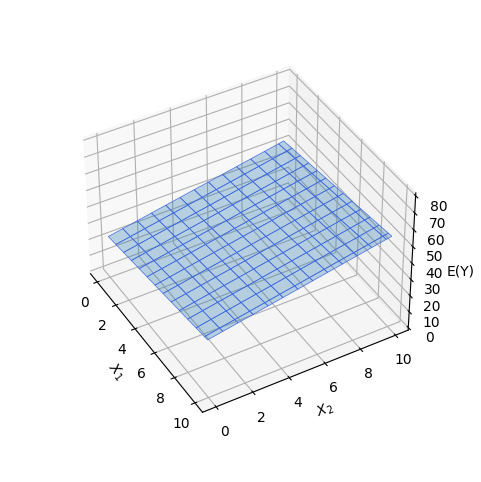
可從圖片看出，在 X１ 固定下，若 X２ 增加 １ 單位，則 EY 增加為 Ｂeta２ 單位；對若 X１ 增加亦同理。而殘差為真實值與預測出來的值（在反應函數）之間的差距。繪圖的程式碼如下。

# https://jakevdp.github.io/PythonDataScienceHandbook/04.12-three-dimensional-plotting.html

import numpy as np
import matplotlib.pyplot as plt

def f(x1, x2, beta):
  return beta[0] + beta[1] * x1 + beta[2] * x2

x1 = np.linspace(0, 10, 100)
x2 = np.linspace(0, 10, 100)
beta = np.array([24, 1, 2])

X, Y = np.meshgrid(x1, x2)
Z = f(X, Y, beta)

fig = plt.figure(figsize=(6, 6))
ax = plt.axes(projection='3d')

# Plot the 3D surface
ax.plot_surface(X, Y, Z, edgecolor='royalblue', lw=0.5, rstride=8,\
                cstride=8, alpha=0.3)
                
ax.set_xlabel(r'$X_1$')
ax.set_ylabel(r'$X_2$')
ax.set_zlabel(r'E(Y)')
ax.set_zlim([0, 80])

# Set zoom and angle view
ax.view_init(400, -30, 0)
ax.set_box_aspect(None, zoom=0.8)

廣義線性回歸（General Linear Regression Model, GLM）

廣義線性回歸模型係簡單線性回歸模型的延伸，前者比後者加入了更多的解釋變數。定義廣義線性回歸模型

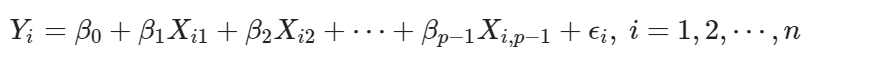
若設 Xi0 = 0，則模型可以寫作

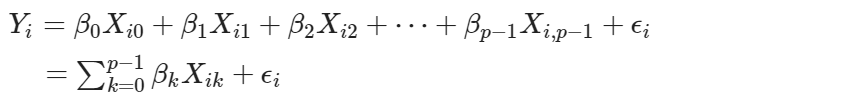
將上式模型以矩陣型式表達，改寫為

小結

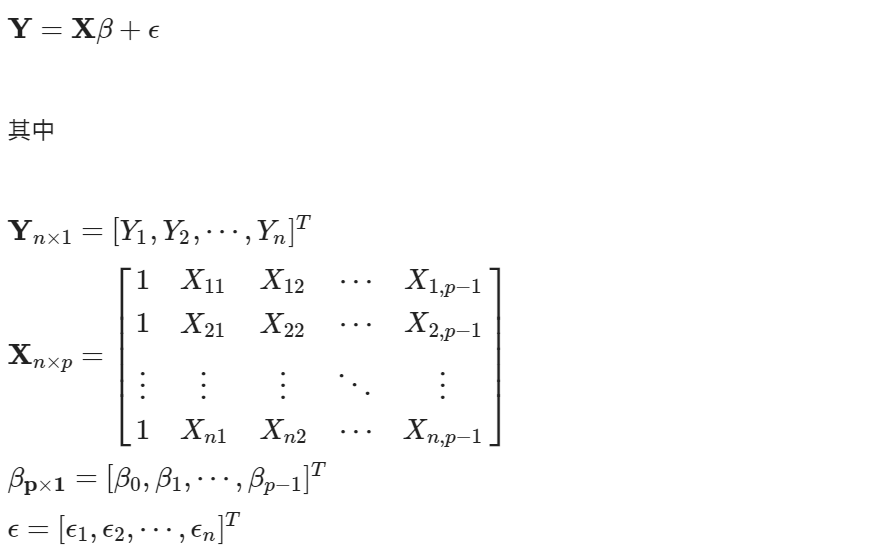
本文從一開始以簡單的模型說明模型參數的意涵，再增加解釋變數，介紹廣義線性回歸模型，及模型不同型式的表達數學式。利用最小平方法計算模型的回歸係數的估計量，讓模型參數有一個數學計算方式。

參考資料：
Michael H. Kutner, Christopher J. Nachtsheim, John Neter, and William Li (2019), Applied Linear Statistical Models. McGraw Hill, New York.